MATEMATIKA
1. Dapatkan luas bidang datar dan
centroidnya (titik berat) yang diarsir berikut dengan integral :
Jawab :
Y = X
2
Luas = -6∫0
(X/2) dx + o∫12 (X/2) dx
=
(x² / 4) 0 + ( x ² / 4) 12
-6 0
= (-6)²
+ (12)²
4 4
= 36 + 144
4 4
= 9 + 36 =
45
∫xy dx
= -6 ∫0 x (x)
dx + 0∫12 x (x) dx
2 2
= -6∫0 x²
dx
+ 0∫12 x²
dx
2 2
= x3 0
+ x2 12
6 -6
6 0
= (-6)3 + (12)3
6 6
= – 216 + 1728
6
6
= – 36
+ 288 = 252
X’ = ∫
x y dx = 252 = 5,6
∫ y dx 45
∫ y2 dx = -6 ∫0 (x)2 dx + 0
∫12 (x)2 dx
2 2
= -6 ∫0 x2 dx + 0
∫12 x2 dx
4 4
= x3 0
+
x3 12
12
–6 12 0
= ( –6)3 + (12)3
12 12
= –216 + 1728
12 12
= –18 + 144 = 126
Y’ = 1/
2 ∫ y2 dx =
1/2. 126
∫ y dx 45
= 1,4
Jadi titik Centroidnya adalah ( 5,6 & 1,4)
2. Dapatkan
luas bidang datar dan centroidnya (titik berat) yang diarsir berikut dengan
integral :
Y = –X
2
L = –4 ∫0 –x dx – 0
∫2 –x dx
2 2
= ( –x)2 0
– ( –x)2 2
4 - 4 4
0
= –
(–4)2 – (– 2)2
4 4
= –4 + 1
= –3
∫x y dx = –4 ∫0 x (–X) dx – 0 ∫2 x (–X) dx
2 2
= –4 ∫0 –x2 dx
– 0 ∫2 –x2 dx
2 2
= (–x3 ) 0
– (–x)3 2
6
–4 6 0
= –(- 4)3 – (–(2)2
6 6
= 64 – (–8) = 64
+ 8= 12
6 6 6
6
X’ = ∫ x y dx
= 12 = –4
∫ y dx
–3
∫ y2 dx
= –4 ∫0 (–x)2 dx – 0 ∫ 2 (–x)2
dx
2 2
= -4 ∫0 x2 dx – 0 ∫2 x2 dx
4 4
=
x3 0 – x3 2
12 -4 12 0
= – 64 – 8
12 12
= – 6
Y’ = ½ ∫ y2 dx
= 1/2 – 6 = 1
∫ y dx –3
Jadi titik Centroidnya = (- 4
, 1 )
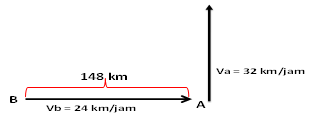
3. Sebuah kapal A
terletak 148 km disebelah timur kapal B bergerak ke utara dengan kecepatan 32
km/jam pada waktu yang sama ,kapal B berlayar kearah timur dengan kecepatan 24
km/jam .bila kedua kapal tersebut melanjutkan perjalanannya ,kapan mereka berada pada jarak pisah yang
terdekat dan berapa jarak tsb ?
Jawab :
a. Kapal – kapal saling menjauh
setelah 1 jam :
Kapal A s = V.t
= 24 x 1
= 24 km
Kapal B s = V.t
= 32 x 1
= 32 km
= X² + Y² = Z²
= 2 X dx
+ 2 Y dx = 2 Z dz
dt dt dt
= ( 2 x32 x 32) +
(2 x 24 x 24)= 2 x 40 dz
Dt
= 2048 + 1152 = 80
dz
dt
=
3200 = 80 dz
dt
= dz = 3200 = 40 km/jam
dt 80
Jadi dz = 40 km/jam dan kapal – kapal saling - menjauh
dt
4. Sebuah kotak tertututp dengan alas
bujur sangkar mempunyai volume 2000 dm³.biaya
pembuatan tutup dan alas adalah Rp. 1.5 /dm² .dapatkan ukuran kotak tsb agar
biaya pambuatan nya minimum.
Jawab :
2 bujur sangkar t persegi panjang =
200
2 x (sisi x sisi) + (sisi x t x 4 ) =
200
2 s² x 4 s
t = 100
Biaya minimum Y = s² + 2 s t + 100 =0
Y’= 2s + 2 t.
2s = 2t
s=t
maka : 2s² + 4 s t = 200
2s² + 4 s² = 200
6 s² =200
s² =√ 200 /6
s =2.357
5. Suatu kotak empat persegi panjang
terbuka dengan ujung-ujung bujur sangkar dengan volume 216 cm³. Harus dibuat
dengan biaya ; $ 50 per cm² untuk dasarnya dan $ 25 per cm² untuk sisinya.cari
ukuran yang paling ekonomis.
Jawab :
V = a x a x b
216 = a² x
b ………………1)
Untuk dasar ► a x b = 50 …………2)x
2
Untuk sisi ► 2(a x b)+ 2a² = 25 ……...3)
Persamaan 1) + 2) :
2 ( a x b ) = 100
2 ( a x b ) + 2 a² = 25
–
2 a² = 75
a² = 37.5
a = √ 37,5
a = 6.12 cm
persamaan …. 1 )
216 = a²
x b
216 =
37.5 x b
B
= 216 / 37.5
B
= 5.76 cm
6. Diketahui fungsi
polynomial y = X³–3X²–45X + 15. Cari :
titik beloknya serta titik mimimumnya / maximumnya dan gambar Grafik fungsinya
Penyelesaian :
Y = X³–3X²–45X + 15
Y’
= 3X²–6X–45
= X² –
2X – 15
= ( X + 3
) ( X – 5 )
= X1 =
– 3 atau X2 = 5
Y”= 6X – 6
untuk X1 = – 3
= 6 (–3) – 6
= – 24
Jadi – 24 < O , Maximum,
Y”
= 6X – 6 untuk
X2 = 5
=
6 (5) – 6
= 24
Jadi 24 > O , Minimum
Y = X³–3X²–45X +
15 untuk X= –3
= (–3)³– 3(–3)²–45(–3)+ 15
= –27–27+135 + 15
= 96 (Nilai Maximum)
Maka titik maximumnya (-3,96)
Y = X³–3X²–45X + 15 untuk X=5
= (5)³–
3(5)²–45(5)+ 15
=
125–75–225+5
= –160
( Nilai Minimum)
Maka titik minimumnya (5,-160)
Tabel : y = X³–3X²–45X + 15
Y
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
||||||
x
|
83
|
96
|
85
|
56
|
15
|
-32
|
-79
|
-120
|
4
|
5
|
6
|
|
-149
|
-170
|
3
|
7. Cari persamaan garis
singgung dan garis normal pada y = X³–2X²
+ 4 di (2,4)
Jawab :
(X0 ,Y0 ) = (2 ,
4)
F(X) = X³–2X² + 4
F’(X) = 3X²–4X
F’(Xo) = F’(2) = 3X²–4X
= 3 (2)²–4 (2)
F’ (Xo) = 12 – 8 = 4
Persamaan Garis Singgung :
Y – Yo = F’(Xo) (X-Xo)
Y –
4 = 4 ( X- 2 )
Y
= 4X – 8 + 4
= 4X – 4
Persamaan Garis Normal :
Y – Yo = –1 (X – Xo)
F’(Xo)
Y – 4 =
–1 (X – 2 )
4
Y =
–X + 2 + 16
4
Y = –X + 18
4
8. Seorang didalam perahu
dayung di A , 10 km dari titik terdekat
P pada pantai yang lurus , ingin mencap ai titik B ,14 km dari P diukur
sepanjang pantai ,dalam waktu sesingkat mungkin . dimana orang tsb harus mendarat bila ia dapat mendayung 3 km/jam dan berjalan 6 km /jam ?
Jawab :
Mendayung : V
= 3 km/jam
t = 1
jam
s =
V.t
s = 3 x
1 =
3 km
Berjalan = :
V = 6 km/jam
t
= 1 jam
s = V.t
s = 6 x
1 =
6 km
Orang itu sama-sama mendapat pada
jarak 6 km ,dengan syarat waktu B = 2.A
9. Cari persamaan garis
singgung dan garis normal pada kurva y =
X³–2X² + 4 di titik (1,5)
Jawab :
( Xo , Yo )
= ( 1 , 5 )
F(X) = X³–2X² + 4
F’(X) = 3X²–4X
F’(Xo) = F’(1) = 3X²–4X
= 3 (1)²–4 (1)
F’ (Xo) = 3 – 4 = –1
Persamaan Garis Singgung :
Y – Yo = F’(Xo) (X-Xo)
Y –
5 = –
1 ( X- 1 )
Y
= – X + 1 + 5
= – X + 6 6–X
Persamaan Garis Normal :
Y – Yo = –1
(X – Xo)
F’(Xo)
Y – 5 = –1
(X – 1 )
–1
Y = X +
4
Tidak ada komentar:
Posting Komentar